Линии. Как ни странно, но в трёхмерной графике они используются достаточно редко. Исключением может служить разве что wireframe-рендеринг, однако даже он порой обходится без, непосредственно, рисования линий. Но так или иначе линии относятся к теме растеризации и я хочу рассказать про них в том числе. Бóльшая часть статьи посвещена описанию разных алгоритмов, но дабы сделать её более информативной, в конце я напишу бенчмарк и сравню алгоритмы по производительности. Пойдём от простого к сложному.
Я не знаю какое название ему придумать для отражения всей сути, но это самый очевидный алгоритм, который приходит мне в голову:
void DrawLine_Dumb(Surface* surface, int x0, int y0, int x1, int y1, u32 color)
{
int dx = x1 - x0; /* - расстояние между точками (дельта) */
int dy = y1 - y0;
f32 length = sqrt((dx * dx) + (dy * dy)); /* - длина линии */
f32 angle = atan2(dy, dx); /* - угол между точками */
f32 s = sin(angle); /* - синус/косинус угла */
f32 c = cos(angle);
for (int i = 0; i < length; ++i) { /* идем вдоль длины линии */
int x = x0 + (int)(i * c); /* считаем координаты x y */
int y = y0 + (int)(i * s);
DrawPoint(surface, x, y, color);
}
}Этот код очень медленный и имеет заметные погрешности в виду ограниченной точности стандартных тригонометрических функций. Его можно оптимизировать, пойдя на разные хитрости и создав lookup table для синусов и косинусов, однако у меня нет желания заниматься оптимизацией изначально плохого алгоритма. Лучше пойдем дальше и посмотрим, какие варианты у нас есть ещё.
Этот метод похож на предыдущий, но теперь мы не используем тригонометрические функции и заранее просчитываем инкрименанты:
void DrawLine_DDA(Surface* surface, int x0, int y0, int x1, int y1, u32 color)
{
int dx = x1 - x0;
int dy = y1 - y0;
int length = max(abs(dx), abs(dy));
if (length > 0) {
f32 ix = (f32)dx / length;
f32 iy = (f32)dy / length;
f32 x = x0 + 0.5;
f32 y = y0 + 0.5;
for (int i = 0; i < length; ++i) {
DrawPoint(surface, floor(x), floor(y), color);
x += ix;
y += iy;
}
}
}Данный код на порядок производительнее предыдущего, но в нем всё ещё присутсвует много манипуляций с двоичными числами. Полностью решить эту проблему поможет Алгоритм Брезенхема.
Пожалуй самый известный и наиболее часто используемый:
void DrawLine_Bresenham(Surface* surface, int x0, int y0, int x1, int y1, u32 color)
{
int dx = ABS(x1 - x0);
int dy = ABS(y1 - y0);
int sx = x0 < x1 ? 1 : -1;
int sy = y0 < y1 ? 1 : -1;
int ed = (dx > dy ? dx : -dy) / 2;
while (x0 != x1 || y0 != y1){
DrawPoint(surface, x0, y0, color);
int e = ed;
if (e >-dx) { ed -= dy; x0 += sx; }
if (e < dy) { ed += dx; y0 += sy; }
}
}
Может быть моя реализация не самая каноничная, в угоду меньшему колличеству строк, но идея в том, что каждый шаг мы вычисляем ошибку - расстояние между координатой и пикселем, сравнивая которую с дельтой решаем, какую из координат инкременировать. Одно из приемуществ этого алгоритма - это отсутствие манипуляций с двоичными числами. Однако теперь во время цикла происходит много операций сравнения.
Название говорит само за себя. Вычислений относительно мало и все они находятся за циклом:
void DrawLine_EFLA(Surface* surface, int x0, int y0, int x1, int y1, u32 color)
{
int dy = y1 - y0;
int dx = x1 - x0;
int yLonger = ABS(dy) > ABS(dx);
if (yLonger) { SWAP(dx, dy); }
int length = dx;
int di;
if (dx < 0) { di = -1; dx = -dx; } else { di = 1; }
f64 fi = (f64)dy;
if (dx != 0) { fi /= dx; }
f64 j = 0;
if (yLonger) {
for (int i = 0; i != length; i += di, j += fi) {
DrawPoint(surface, x0 + (int)j, y0 + i, color);
}
} else {
for (int i = 0; i != length; i += di, j += fi) {
DrawPoint(surface, x0 + i, y0 + (int)j, color);
}
}
}
Принцип отличается от предыдущих алгоритмов. В первую очередь мы определеяем, по какой оси линия длиннее. Если ось "y" длинне, меняем между собой значения dx и dy - таким образом dx всегда будет длиннее dy. Далее находим целочисленный и двоичный инкременант, и в зависимости от того, какую из осей мы определили длиннейшей, по такой оси и будет целочистенный инкрименант - идем вдоль него и рисуем точки.
Я написал программу для тестирования, исходники которой прикладываю ниже:
int main(int argc, char** argv)
{
const int c = 5000000;
for (int test = 0; test < 4; ++test)
{
u32 start = GetTickCount();
int w = framebuffer.width / 2;
int h = framebuffer.height / 2;
int x = w * (test / 2);
int y = h * (test % 2);
int i = c;
static const char* name = "";
switch (test) {
case 0: name = "DrawLine_Dumb";
while (--i) DrawLine_Dumb(&framebuffer,
x + (i / w) % w, y + (i / h) % h, x + (i % w), y + (i % h), i);
break;
case 1: name = "DrawLine_DDA";
while (--i) DrawLine_DDA(&framebuffer,
x + (i / w) % w, y + (i / h) % h, x + (i % w), y + (i % h), i);
break;
case 2: name = "DrawLine_Bresenham";
while (--i) DrawLine_Bresenham(&framebuffer,
x + (i / w) % w, y + (i / h) % h, x + (i % w), y + (i % h), i);
break;
case 3: name = "DrawLine_EFLA";
while (--i) DrawLine_EFLA(&framebuffer,
x + (i / w) % w, y + (i / h) % h, x + (i % w), y + (i % h), i);
break;
}
u32 end = GetTickCount();
printf("%*s draw %d lines @ %.3f seconds\n", 20, name, c, (f64)(end - start) / 1000.0);
}
return 0;
}
В этом тесте мы рисуем пять миллионов линий каждым из алгоритмов и замеряем затраченное на это время.
Тест запускался на машине Windows 10, Intel Core i5-4210M @ 2.60 GHz, компилятор MSVC 14.10.25017 x64:
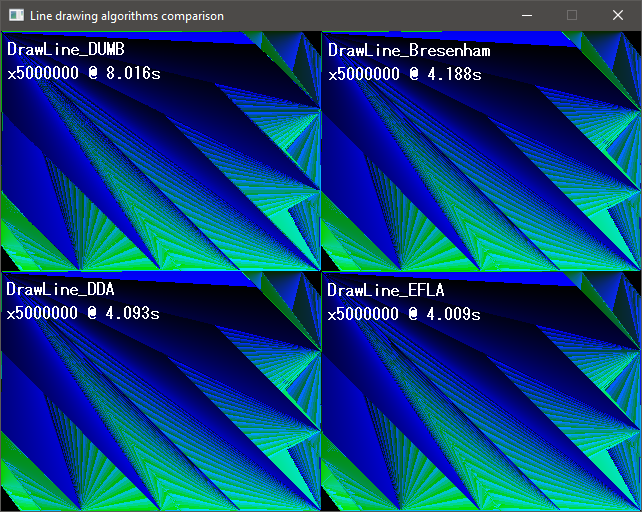
DrawLine_Dumb draw 5000000 lines @ 8.016 seconds
DrawLine_DDA draw 5000000 lines @ 4.093 seconds
DrawLine_Bresenham draw 5000000 lines @ 4.188 seconds
DrawLine_EFLA draw 5000000 lines @ 4.009 seconds
В заключение хотелось бы сказать, что результат тестов меня удивил, поскольку в моей реализации алгоритм DDA на разных компиляторах и машинах оказывался чуть быстрее EFLA. Вероятно это связано с архитектурой совмеренных процессоров и микро-оптимизациями, которые происходят у них внутри.
Это была первая статья из цикла по разрабоке софтверного рендерера. В дальнейшем я расскажу про рисование треугольников и матричные преобразования.