Софтверная растеризация: быстрый и точный алгоритм растеризации треугольников на C
Translation of this article in English
Основа трехмерной графики - растеризация треугольников. В этой статье я объясню как работает алгоритм софтверной растеризации треугольников в моём игровом движке.
Сперва я представлю сам алгоритм в его конечном виде, а затем мы разберём его поподробнее:
static void SwapFloat(float* a, float* b) { float c = *a; *a = *b; *b = c; }
void DrawTriangle(
float ax, float ay, float az, float au, float av,
float bx, float by, float bz, float bu, float bv,
float cx, float cy, float cz, float cu, float cv
) {
// For every vertex:
// x, y - screen coordinates
// z - depth
// u, v - texture coordinates
// Sort vertices by y-coordinate ascending (y1 <= y2 <= y3)
if (ay > by) {
// swap(a, b)
SwapFloat(&ax, &bx);
SwapFloat(&ay, &by);
SwapFloat(&az, &bz);
SwapFloat(&au, &bu);
SwapFloat(&av, &bv);
}
if (ay > cy) {
// swap(a, c)
SwapFloat(&ax, &cx);
SwapFloat(&ay, &cy);
SwapFloat(&az, &cz);
SwapFloat(&au, &cu);
SwapFloat(&av, &cv);
}
if (by > cy) {
// swap(b, c)
SwapFloat(&bx, &cx);
SwapFloat(&by, &cy);
SwapFloat(&bz, &cz);
SwapFloat(&bu, &cu);
SwapFloat(&bv, &cv);
}
// Round y-coordinates and clamp to screen bounds
int y_min = max( (int)ceilf(ay - 0.5f), 0);
int y_mid = min(max((int)ceilf(by - 0.5f), 0), screen_height);
int y_max = min( (int)ceilf(cy - 0.5f), screen_height);
// Prepare values for perspective-correct interpolation
az = 1.0f / az;
bz = 1.0f / bz;
cz = 1.0f / cz;
au *= az;
av *= az;
bu *= bz;
bv *= bz;
cu *= cz;
cv *= cz;
// Rasterize triangle scanlines
for (int y = y_min; y < y_max; y++) {
float pixel_center = (float)y + 0.5f;
float lt, lx, lz, lu, lv; // left edge
float rt, rx, rz, ru, rv; // right edge
// Calculate left edge
lt = (pixel_center - ay) / (cy - ay);
lx = ax + (cx - ax) * lt;
lz = az + (cz - az) * lt;
lu = au + (cu - au) * lt;
lv = av + (cv - av) * lt;
// Determine if we are in the first or the second half of the triangle
if (y < y_mid) {
// Calculate right edge (first half)
rt = (pixel_center - ay) / (by - ay);
rx = ax + (bx - ax) * rt;
rz = az + (bz - az) * rt;
ru = au + (bu - au) * rt;
rv = av + (bv - av) * rt;
} else {
// Calculate right edge (second half)
rt = (pixel_center - by) / (cy - by);
rx = bx + (cx - bx) * rt;
rz = bz + (cz - bz) * rt;
ru = bu + (cu - bu) * rt;
rv = bv + (cv - bv) * rt;
}
// Ensure "l" is always to the left of "r"
if (lx > rx) {
// swap(l, r)
SwapFloat(&lx, &rx);
SwapFloat(&lz, &rz);
SwapFloat(&lu, &ru);
SwapFloat(&lv, &rv);
}
// Round x-coordinates and clamp to screen bounds
int ilx = (int) ceilf(lx - 0.5f); // top-left rule: ceil to include left edge
int irx = (int)floorf(rx - 0.5f); // top-left rule: floor to exclude right edge
int x_min = max(ilx, 0);
int x_max = min(irx + 1, screen_width);
// Loop over the horizontal range of the current scanline
for (int x = x_min; x < x_max; x++) {
int i = (y * screen_width) + x;
float t = (float)(x - ilx) / (rx - lx);
float z = lz + (rz - lz) * t;
if (z > screen_depth[i]) {
float u = (lu + (ru - lu) * t) / z;
float v = (lv + (rv - lv) * t) / z;
screen_color[i] = SampleTextureColor(texture, u, v);
screen_depth[i] = z;
}
}
}
}
Разбор алгоритма
Начнем с того, что наметим план действий. Наша цель - самым эффективным образом закрасить пиксели внутри треугольника, избежав избыточных вычислений.
Сразу отметим, что рисовать пиксели внутри треугольника нам стоит строка за строкой, начиная с верхнего-левого угла, потому что таким образом пиксели хранятся в оперативной памяти. Мы хотим избежать "прыжков" по оперативке и проходиться по буферу линейно - это залог хорошей оптимизации.
Мы должны рассчитать переменные для цикла, по которым мы будем двигаться вдоль оси y и заливать пиксели между гранями треугольника, но сперва нужно подготовить сами вершины.
Шаг 1: Отсортируем вершины по y-координате
if (ay > by) { SwapPoint(&a, &b); }
if (ay > cy) { SwapPoint(&a, &c); }
if (by > cy) { SwapPoint(&b, &c); }
Сортировка нужна, чтобы упростить проход по треугольнику. Мы будем предполагать, что a - верхняя вершина, b - средняя, c - нижняя. Это позволит разбить треугольник на две части: верхнюю и нижнюю - так нам проще будет рассчитывать начало и конец горизонтального отрезка, поскольку левая и правая грани будут строго прямыми.
Шаг 2: Top-left filling convention (правило верхнего левого угла)
Очень важный момент, который иногда упускается из внимания: правило растеризации. Дело в том, что если мы хотим избежать "щелей" между соседними треугольниками, то важно придерживаться единого принципа, по которому мы будем округлять координаты. В DirectX и Vulkan принято правило: пиксель считается покрытым, если центр пикселя лежит внутри треугольника. В нашем алгоритме мы тоже будем его придерживаться. Для этого мы округляем y - 0.5 вверх, чтобы учесть центр пикселя:
int y_min = (int)ceilf(ay - 0.5f);
int y_mid = (int)ceilf(by - 0.5f);
int y_max = (int)ceilf(cy - 0.5f);
Забегая чуть вперед, тоже самое мы будем делать и при округлении координаты x, но там мы будем рисовать левый край включительно, и исключать правый край, округляя его вниз:
int ilx = (int) ceilf(lx - 0.5f); // top-left rule: ceil to include left edge
int irx = (int)floorf(rx - 0.5f); // top-left rule: floor to exclude right edge
Придерживаясь таких правил мы избавимся от зазоров между полигонами. Особенно важно это учитывать, если вы собираетесь использовать софтверный растеризатор для отсечения окклюзий (например при реализации алгоритма Hierarchical Depth Buffer).
Шаг 3: Подготовка к интерполяции с учетом перспективы
az = 1.0f / az;
bz = 1.0f / bz;
cz = 1.0f / cz;
Инверсия z-координат позволит нам выполнить перспективно-корректную интерполяцию. Если мы не будем этого делать, то при вычислении UV-координат получим эффект растягивающихся текстур с PS1 - если цель достичь именно такого стилистичего эффекта, то можно намеренно пропустить этот шаг.
Шаг 4: Проход по сканлайнам (вдоль координаты y)
for (int y = y_min; y < y_max; y++) {
...
}
В этом цикле мы пойдем сверху вниз вдоль каждой строки, рассчитаем начало и конец горизонтального отрезка, и отрисуем его.
Шаг 5: Вычисление начала и конца горизонтального отрезка
В каждой строке вычисляем координаты x для начала и конца отрезка:
lt = (pixel_center - ay) / (cy - ay);
lx = ax + (cx - ax) * lt;
lz = az + (cz - az) * lt;
lt - это параметр линейной интерполяции вдоль левой грани. Левая грань всегда a → c
if (y < y_mid) {
rt = (center_y - ay) / (by - ay);
rx = ax + (bx - ax) * rt;
rz = az + (bz - az) * rt;
// ...
} else {
rt = (center_y - by) / (cy - by);
rx = bx + (cx - bx) * rt;
rz = bz + (cz - bz) * rt;
// ...
}
rt - это параметр линейной интерполяции вдоль правой грани. Правая грань может быть либо a → b (верхняя половина треугольника), либо b → c (нижняя половина). Это определяется по y < y_mid.
Шаг 6: Гарантия порядка лево-право
if (lx > rx) { SwapFloat(&lx, &rx); SwapFloat(&lz, &rz); }
В треугольнике есть как длинная грань (a → c), так и две других, через которые проходит линия разделения по y_mid. Мы заранее не определяли с какой стороны находится длинная грань, потому что это не имеет значения при вычислении координат, но имеет при отрисовке. Поэтому после того, как мы вычислили координаты для левой и правой грани, мы просто убедимся, что координаты l всегда левее r.
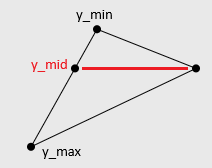
Шаг 7: Растеризация строки
Теперь проходим по пикселям от lx до rx (округляя их по правилам растеризации) и выполняем линейную интерполяцию глубины:
for (int x = x_min; x < x_max; x++) {
int i = (y * screen_width) + x;
float t = (float)(x - ilx) / (rx - lx); // фактор по x (0.0 - начало отрезка, 1.0 - конец)
float z = lz + (rz - lz) * t; // значение глубины (интерполяция между левым и правым краем)
if (z > screen_depth[i]) { // пиксель закрашивается, если он ближе к камере, чем предыдущий
screen_color[i] = 0xFFFFFF;
screen_depth[i] = z;
}
}
Шаг 8: Дополнительные параметры вершин
В этой статье вершины имели 5 параметров: x, y, z, u, v.
x y - для положения в экранном пространстве
z - для глубины
u v - для текстурных координат
Но ничего не мешает расширить этот метод и добавить новые параметры вершин. К примеру, вы можете добавить параметр l, который будет отвечать за затухание цвета текстуры - это позволит реализовать повертексное освещение. Вы можете добавить ещё одну пару uv координат для мультитекстурирования или лайтпамов. Всё это делается всего лишь добавлением новых параметров, по аналогии с z или uv.
Этот алгоритм расширяемый и все вычисления в нём работают по одинаковому принципу.
Шаг 9: Оптимизация
Я намеренно упростил код, представленный в начале статьи, чтобы улучшить его читабельность в угоду производительности. Если вы дочитали до этого момента и вас интересует дальнейшая оптимизация, то ниже вы найдете финальную версию алгоритма для реального рендерера:
static void DrawTriangle_Span(
const Texture *texture,
int y,
float lx, float lz, float la, float lb, float lc,
float rx, float rz, float ra, float rb, float rc
) {
// Ensure "l" is always to the left of "r"
if (lx > rx) {
SwapFloat(&lx, &rx);
SwapFloat(&lz, &rz);
SwapFloat(&la, &ra);
SwapFloat(&lb, &rb);
SwapFloat(&lc, &rc);
}
// Precalculate spans
float span_x = rx - lx;
if (span_x <= 0.0f) {
return; // skip if no pixels to draw
}
float span_z = rz - lz;
float span_a = ra - la;
float span_b = rb - lb;
float span_c = rc - lc;
// Round and x-coordinates to screen bounds
int ilx = (int) ceilf(lx - 0.5f); // top-left rule: ceil to include left edge
int irx = (int)floorf(rx - 0.5f); // top-left rule: floor to exclude right edge
int nlx = max(ilx, 0);
int nrx = min(irx + 1, screen_width);
// Get scanline pointers
int i = (screen_width * y) + nlx;
WORD *color_ptr = &screen_color[i];
float *depth_ptr = &screen_depth[i];
// Loop over the horizontal range of the current scanline
for (int x = nlx; x < nrx; x++) {
// Interpolate z
float t = (float)(x - ilx) / span_x;
float z = lz + span_z * t;
// Depth test
if (z > *depth_ptr) {
// Perspective-correct interpolation
float u = (la + span_a * t) / z;
float v = (lb + span_b * t) / z;
float l = (lc + span_c * t) / z;
// Sample texture color
WORD color = SampleTexture(texture, u, v);
// Transparency-bit test
if (color & COLOR16_MASK_A) {
// Apply lighting
color = Color_ApplyLighting(color, l);
*color_ptr = color;
*depth_ptr = z;
}
}
// Step scanline pointers
color_ptr++;
depth_ptr++;
}
}
void DrawTriangle(
const Texture *texture,
float x1, float y1, float z1, float a1, float b1, float c1,
float x2, float y2, float z2, float a2, float b2, float c2,
float x3, float y3, float z3, float a3, float b3, float c3
) {
// Prepare the triangle vertices for perspective-correct texture interpolation
z1 = 1.0f / z1;
z2 = 1.0f / z2;
z3 = 1.0f / z3;
a1 *= z1;
b1 *= z1;
c1 *= z1;
a2 *= z2;
b2 *= z2;
c2 *= z2;
a3 *= z3;
b3 *= z3;
c3 *= z3;
// Sort vertices by y-coordinate ascending (y1 <= y2 <= y3)
if (y1 > y2) {
SwapFloat(&x1, &x2);
SwapFloat(&y1, &y2);
SwapFloat(&z1, &z2);
SwapFloat(&a1, &a2);
SwapFloat(&b1, &b2);
SwapFloat(&c1, &c2);
}
if (y1 > y3) {
SwapFloat(&x1, &x3);
SwapFloat(&y1, &y3);
SwapFloat(&z1, &z3);
SwapFloat(&a1, &a3);
SwapFloat(&b1, &b3);
SwapFloat(&c1, &c3);
}
if (y2 > y3) {
SwapFloat(&x2, &x3);
SwapFloat(&y2, &y3);
SwapFloat(&z2, &z3);
SwapFloat(&a2, &a3);
SwapFloat(&b2, &b3);
SwapFloat(&c2, &c3);
}
// Round y-coordinates and clamp to screen bounds
int y_min = max( (int)ceilf(y1 - 0.5f), 0);
int y_mid = min(max((int)ceilf(y2 - 0.5f), 0), screen_height);
int y_max = min( (int)ceilf(y3 - 0.5f), screen_height);
// Precalculate edges
float dy13 = y3 - y1;
float dx13 = x3 - x1;
float dz13 = z3 - z1;
float da13 = a3 - a1;
float db13 = b3 - b1;
float dc13 = c3 - c1;
float dy12 = y2 - y1;
float dx12 = x2 - x1;
float dz12 = z2 - z1;
float da12 = a2 - a1;
float db12 = b2 - b1;
float dc12 = c2 - c1;
float dy23 = y3 - y2;
float dx23 = x3 - x2;
float dz23 = z3 - z2;
float da23 = a3 - a2;
float db23 = b3 - b2;
float dc23 = c3 - c2;
#pragma omp parallel
{
// Draw the top part of the triangle
#pragma omp for
for (int y = y_min; y < y_mid; y++) {
float pixel_center = (float)y + 0.5f;
float lt = (pixel_center - y1) / dy13;
float rt = (pixel_center - y1) / dy12;
DrawTriangle_Span(
texture, y,
x1 + dx13 * lt,
z1 + dz13 * lt,
a1 + da13 * lt,
b1 + db13 * lt,
c1 + dc13 * lt,
x1 + dx12 * rt,
z1 + dz12 * rt,
a1 + da12 * rt,
b1 + db12 * rt,
c1 + dc12 * rt
);
}
// Draw the bottom part of the triangle
#pragma omp for
for (int y = y_mid; y < y_max; y++) {
float pixel_center = (float)y + 0.5f;
float lt = (pixel_center - y1) / dy13;
float rt = (pixel_center - y2) / dy23;
DrawTriangle_Span(
texture, y,
x1 + dx13 * lt,
z1 + dz13 * lt,
a1 + da13 * lt,
b1 + db13 * lt,
c1 + dc13 * lt,
x2 + dx23 * rt,
z2 + dz23 * rt,
a2 + da23 * rt,
b2 + db23 * rt,
c2 + dc23 * rt
);
}
}
}
Спасибо за уделённое внимание! Буду рад, если вы найдете применение этому алгоритму в своих проектах.